Outils du BIN

2. L'importance des tests

«Es-tu sûr.e que ça marche ?».

Se faire poser cette question peut faire peur si notre code n’a pas été testé en profondeur. Au mieux, pourra-t-on répondre «je pense que oui» ou bien «ça semble marcher», ce qui n’est pas susceptible de convaincre notre interlocuteur. De bonnes pratiques en matière de tests peuvent soulager (en partie) cette peur.

Dans ce guide, nous répondrons à la question de savoir comment tester son code afin de s’assurer de sa robustesse.

L’information contenue dans ce guide provient principalement de deux ouvrages de référence :

1. Clean Code: A Handbook of Agile Software
   Craftsmanship
2. Introduction to software testing

Motivation

Tester son code prend du temps. Le faire nous oblige parfois à écrire plus de code pour tester notre programme que le code contenu dans le programme lui-même. Pourquoi donc devrait-on prendre le temps de bien tester notre code? Pour plusieurs raisons :

1. Notre code sera plus facile à réusiner (refactor) : pour garder son code propre, il est nécessaire de le réusiner (extraire des fonctions, réorganiser la structure de nos fonctions, renommer des variables, etc.). Lorsque nous n’avons pas de tests, ces opérations peuvent paraître terrifiantes. Est-ce que je vais briser mon code en le réusinant? Cette peur peut nous décourager de réusiner notre code. À long terme, cela fera en sorte que notre code deviendra sale, difficile à maintenir, à comprendre et à modifier.
2. Notre code sera plus facile à «débugger» : lorsqu’on écrit du nouveau code, il arrive souvent que cela crée des bugs dans notre programme. Lorsqu’on roule un long bout de code, qui fait intervenir de multiples fonctions, et que ce long bout de code n’a pas le comportement attendu, il peut être très pénible de trouver l’emplacement de l’erreur. C’est ce que nous permettent d’éviter les tests. En faisant des tests, on peut plus facilement localiser ce qui a mal tourné dans notre code.
3. Notre code sera mieux structuré : les tests nous forcent à mieux structurer notre code, car il nous force à décomposer notre code en petites fonctions facilement testables. Ce point deviendra sans doute plus clair après la lecture du guide.
4. Notre code sera plus robuste : l’objectif des tests est de détecter s’il y a des bugs dans notre code. Les bugs sont ce que nous voulons éviter. En science des données, nous voulons que nos résultats soient fiables. Pour s’assurer de la qualité de nos résultats, on doit être confiant de la fiabilité de notre code. Du code fiable, on s’en doute, ne contient pas (ou le moins possible) de bugs.

Qu’est-ce qu’un bug ?

On le devine, un des objectifs principaux des tests est de répondre à la question suivante :

Est-ce que mon code contient des bugs?

Mais qu’est-ce qu’un bug?

Cela peut sembler une question triviale, mais elle est plus complexe qu’on peut le penser à première vue.

Voici quelques distinctions qui nous permettront de mieux comprendre ce qu’est un bug. Nous serons mieux en mesure de les détecter avec nos tests par la suite. Les distinctions proposées sont celles entre la faute, l’erreur et l’échec

• Faute : Coquille dans le code écrit. On peut penser à une coquille dans l’écriture d’un nom de variable, ou l’inversion de deux variables.
• Erreur : État interne incorrect causé par une faute. Par exemple, une variable n’a pas la valeur qu’elle devrait avoir.
• Échec : Inadéquation entre le comportement attendu et le comportement observé.
• Bug : Faute → Erreur → Échec. Un bug a lieu lorsqu’une faute cause une erreur qui cause à son tour un échec.

Ce qu’on doit comprendre de ces distinctions c’est qu’il est possible qu’une faute ne cause pas d’erreur et qu’une erreur ne cause pas d’échec. Voyons un exemple de faute sans erreur et d’erreur sans échec.

Faute sans erreur

premier_prenom = "Louis"
premier_nom = "Santerre"

deuxieme_prenom = "Olivier"
deuxieme_nom = "Santerre"

premier_nom_complet = premier_prenom + " " + premier_nom
deuxieme_nom_complet = deuxieme_prenom + " " + premier_nom

Dans la dernière ligne de code, deuxieme_nom_complet = deuxieme_prenom + " " + premier_nom, il y a une coquille. On utilise la variable premier_nom au lieu de deuxieme_nom lorsqu’on construit le deuxieme_nom_complet. Il s’agit d’une faute. Heureusement, les deux noms à former ont le même nom de famille. La valeur de deuxieme_nom_complet est donc la bonne par un coup de chance. Il n’y a pas d’erreur.

Erreur sans échec

def retourne_le_premier_nom(prenom_1, prenom_2, nom_1, nom_2):
    nom_complet_1 = prenom_1 + nom_1
    nom_complet_2 = prenom_2 + nom_1
    return nom_complet_1

Ici, il y a une faute qui cause une erreur dans la ligne de code nom_complet_2 = prenom_2 + nom_1 (si nom_1 n’est pas égal à nom_2 évidemment). nom_complet_2 n’a pas la bonne valeur. Il y a donc un état interne incorrect. Cependant puisqu’en utilisant la fonction retourne_le_premier_nom() nous n’aurons jamais accès au nom_complet_2, il n’y a pas d’échec. L’échec, on le rappelle, a à avoir avec le comportement attendu de la fonction. Avec retourne_le_premier_nom() nous nous attendons à avoir le premier nom complet seulement, le comportement de la fonction sera donc conforme au comportement attendu. (Cette fonction a évidemment été écrite pour servir l’exemple. Les paramètres prenom_2 et nom_2 ne servent à rien).

Une des conclusions que l’on peut tirer de cette distinction est qu’il est impossible de tester directement si notre code contient des fautes ou des erreurs. Nous ne pouvons détecter que les échecs.

Les tests unitaires

Le type de test le plus répandu est le test unitaire. Les tests unitaires testent une unité de code. L’unité en question est la fonction.

Une fonction a généralement une valeur d’entrée et une valeur de sortie. Un test unitaire répond à la question suivante :

Étant donné une (ou des) valeur(s) d’entrée, est-ce que la valeur de sortie est celle attendue?

Comme nous l’avons dit à la fin de la section précédente, le test unitaire ne révèle pas directement les fautes ni les erreurs; seulement les échecs.
Ainsi, pour qu’un test révèle un bug, il doit :

1. Faire rouler le code fautif.
2. Que la faute cause une erreur.
3. Que l’erreur se propage dans la valeur de sortie de la fonction testée.
4. Que le test observe la partie incorrecte de la sortie.

La décomposition de l’espace des entrées

Une des limites des tests unitaires, outre le fait qu’ils ne détectent que les échecs, et qu’ils ne peuvent tester qu’une seule valeur d’entrée à la fois. Le rôle du testeur est de répondre à la question de savoir quelle valeur choisir. C’est à la question de savoir comment faire ce choix que nous répondrons dans cette section.

L’ensemble des combinaisons possibles des valeurs d’entrée que peut prendre une fonction est ce que nous appellerons l’espace des entrées. Plus précisément, la tâche du testeur consiste à diviser l’espace des entrées de manière à maximiser la couverture de l’espace et minimiser la redondance. L’objectif (et la difficulté) est de trouver une manière de diviser l’espace des *entrées de manière à ce que chaque élément d’une région donnée ait une utilité équivalente (éviter la redondance) et de manière à couvrir le plus de cas possibles (maximiser la couverture).
Dans ce qui suit, nous verrons trois manières différentes de diviser l’espace des entrées qui sont complémentaires.

La fonction triangle()

Dans cette section, nous utiliserons la fonction triangle() à titre d’exemple.

La fonction triangle(cote_1, cote_2, cote_2) prend la mesure de trois côtés en paramètre, et nous renvoie en valeur de sortie le type de triangle dont il s’agit. Il y a quatre possibilités, équilatéral, isocèle, scalène ou invalide. La question à laquelle on veut répondre est celle de savoir comment tester la fonction triangle() afin de savoir si elle contient des bugs. Vous pouvez essayer de répondre à cette question avant de passer à la prochaine section.

Division de l’espace basée sur l’interface

Il s’agit de la division de l’espace la plus simple. Ici, on s’intéresse à chaque paramètre pris isolément. On ne s’intéresse pas, à proprement parler, à ce que la fonction est censée faire. On veut plutôt tester les cas limites de chaque paramètre.

Dans le tableau ci-bas se trouve une liste de type de variable avec des critères de division que l’on peut utiliser pour ce type de variable.

Type de paramètre	Critère de division
entier	>= 0
entier	< 0
liste	liste vide
liste	liste avec un élément
liste	liste avec au moins 2 éléments
chaîne de caractère	chaîne vide
chaîne de caractère	chaîne de plusieurs caractères
chaîne de caractère	chaîne de caractères spéciaux
tableau de données	tableau vide
tableau de données	tableau avec des données

Avec notre exemple de triangle() il s’agirait ici de tester ce qui se passe quand la valeur d’un des paramètres est inférieure ou égale à 0 et supérieure à 0. On sait que lorsque la longueur d’un côté d’un triangle est inférieure ou égale à 0, le triangle est invalide. On s’assurera donc que la fonction nous renvoie "invalide" lorsqu’un des paramètres est égal à 0.

On testera aussi que la fonction nous retourne un triangle valide lorsque la valeur de tous les côtés est supérieure à 0. Dans le cas ci-bas, on teste le triangle (1,1,1) qui doit être un triangle équilatéral.

L’exemple ci-bas fait usage de la librairie pytest qui est une librairie permettant de faire des tests unitaires en python. Le nom de la fonction est ce qu’on désire tester de manière générale, et chaque assert représente un test unitaire particulier. Ainsi, assert triangle(0,1,1) == "invalide" pourrait être traduit en langage courant de la manière suivante : assure-toi que la fonction triangle() avec les paramètres (0,1,1) renvoie la valeur invalide.

def test_interface_triangle():
    assert triangle(0,1,1) == "invalide"
    assert triangle(1,0,1) == "invalide"
    assert triangle(1,1,0) == "invalide"
    assert triangle(1,1,1) == "equilatéral"

Division de l’espace basée sur la fonctionnalité

La couverture basée sur l’interface, on s’en doute, ne constitue pas le fin mot de l’affaire. Même en ayant couvert tous les cas d’interface, on n’est pas en mesure de répondre à la question de savoir si notre fonction contient des bugs ou non. La raison est bien simple. Le comportement d’une fonction a généralement à voir avec une certaine combinaison de paramètres. C’est à cela qu’on s’intéresse dans la couverture basée sur la fonctionnalité. Ici, pour générer nos tests, on doit répondre à la question de savoir ce que notre fonction doit faire, et on divisera l’espace des entrées en conséquence.

Dans le cas qui nous intéresse, on voudra voir si la fonction nous retourne le bon type de triangle en fonction des trois côtés passés en paramètre.

La division de l’espace des entrées

Fonction	Critère de division
Invalide	a + b > c ou a + c > b ou b + c > a
Equilatéral	a = b = c
Isocèle	non équilatéral non invalide a = b ou a = c ou b = c
Scalène	non invalide non équilatéral non isocèle

Il suffit ensuite de choisir un représentant par catégorie et de tester si le résultat est le bon.

def test_invalide():
    assert triangle(1,2,1000) == "invalide"

def test_equilateral():
    assert triangle(2,2,2) == "equilatéral"

def test_isocele():
    assert triangle(2,2,1) == "isocèle"

def test_scalene()
    assert triangle(1,2,3) == "scalène"

Division de l’espace basée sur les graphes

La dernière manière de diviser l’espace des entrées s’appuie sur les graphes.
Cette couverture demande de modéliser notre fonction en graphe. L’objectif sera de parcourir tous les chemins possibles du graphe.

Un graphe est un ensemble de noeuds (sommets, points) et de liens (arêtes, lignes) qui expriment des relations entre les noeuds.
Ils sont généralement représentés de la manière suivante :

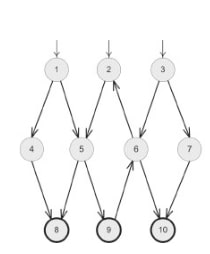
La couverture basée sur les graphes demande qu’on représente certains blocs de code par des noeuds, et les manières de passer d’un bloc à l’autre par des liens. Les différents bloques de code sont divisés par les instructions conditionnelles (if/else). Prenons l’exemple suivant où chaque bloc a été nommé à l’aide de commentaire. La fonction, comme son nom l’indique, vise à déterminer si un nombre est à la fois un nombre pair et un multiple de trois. Elle renvoit True si c’est le cas, et False sinon :

def nombre_est_pair_et_multiple_de_3(x):

  # noeud 1
  modulo_2 = x % 2

  if modulo_2 == 0:
    # noeud 2
    est_pair = True
  else:
    # noeud 3
    est_pair = False

  # noeud 4
  modulo_3 = x % 3

  if modulo_3 == 0:
    # noeud 5
    est_multiple_de_3 = True
  else :
    # noeud 6
    est_multiple_de_3 = False

  # noeud 7
  est_pair_et_multiple_de_3 = est_pair & est_multiple_de_3

  return est_pair_et_multiple_de_3

On pourrait représenter cette fonction par le graphe suivant :

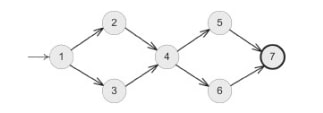
Il y a quatre chemins possibles dans ce graphe :

Chemin 1 : 1 -> 2 -> 4 -> 5 -> 7
Chemin 2 : 1 -> 2 -> 4 -> 6 -> 7
Chemin 3 : 1 -> 3 -> 4 -> 5 -> 7
Chemin 4 : 1 -> 3 -> 4 -> 6 -> 7

Une couverture basée sur les graphes consiste à choisir des valeurs d’entrées de manière à tester tous les chemins possibles.

Dans ce cas les valeurs d’entrée devraient répondre aux conditions suivantes pour passer par chacun des quatre chemins :

Chemin 1 : Est pair et est multiple de trois.
Chemin 2 : Est pair mais n’est pas un multiple de trois.
Chemin 3 : Est impair et est un multiple de trois.
Chemin 4 : Est impair et n’est pas un multiple de trois.

On comprend que seul le chemin 1 nous renvoit la valeur True, et les trois autres chemins nous renvoient la valeur False. Voici donc un exemple de
quatre tests que l’on pourrait faire pour parcourir les quatre chemins du graphe :

def pair_multiple():
    assert nombre_est_pair_et_multiple_de_3(6) == True

def pair_non_multiple():
    assert nombre_est_pair_et_multiple_de_3(2) == False

def impair_multiple():
    assert nombre_est_pair_et_multiple_de_3(3) == False

def impair_non_multiple()
    assert nombre_est_pair_et_multiple_de_3(5) == False

La couverture basée sur les graphes de la fonction triangle()

Revenons, pour finir, sur la fonction triangle(). Admettons que la fonction triangle() est programmée de la manière suivante
(il aurait été possible de la programmer de manière plus efficace, mais nous l’avons programmé de cette manière pour le bien de l’exemple):

def triangle(cote1, cote2, cote3):
  # noeud 1
  type = ""
  if le_triangle_est_invalide(cote1, cote2, cote3):
    # noeud 2
    type = "Invalide"

  elif (cote1 == cote2 & cote2 == cote3):
    # noeud 3
    type = "Equilatéral"

  elif (cote1 == cote2):
    # noeud 4
    type = "Isocèle"

  elif(cote2 == cote3):
    # noeud 5
    type = "Isocèle"

  elif(cote1 == cote3):
    # noeud 6
    type = "Isocèle"

  else:
    # noeud 7
    type = "Scalène"

  #noeud 8
  return type

On pourrait représenter la fonction de la manière suivante :

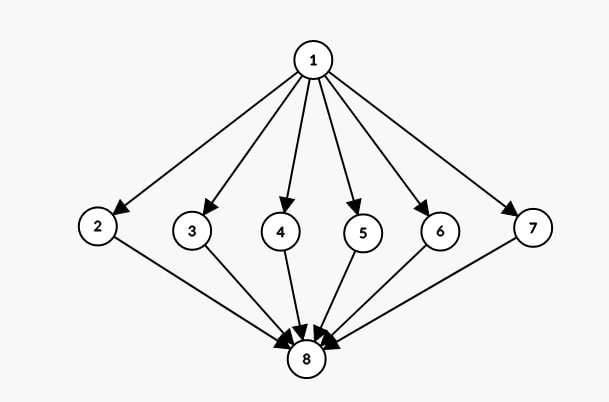
Dans ce cas-ci, on trouve 6 chemins possibles:

Chemin 1 : 1 -> 2 -> 8
Chemin 2 : 1 -> 3 -> 8
Chemin 3 : 1 -> 4 -> 8
Chemin 4 : 1 -> 5 -> 8
Chemin 5 : 1 -> 6 -> 8
Chemin 6 : 1 -> 7 -> 8

Lorsqu’on regarde les tests qui ont été faits dans les sections précédentes. On remarque que les chemins 1, 2, 3 et 6 ont déjà été empruntés,
mais pas les chemins 4 et 5. Pour compléter la couverture basée sur les graphes nous devrions donc ajouter deux tests qui parcourent les chemins
4 et 5 :

def test_isocele_chemin_4():
    assert triangle(2,1,2) == "isocèle"

def test_isocele_chemin_5():
    assert triangle(1,2,2) == "isocèle"

Les bonnes pratiques à respecter pour écrire des tests unitaires

Un des problèmes avec les tests est qu’ils ne sont pas testés. Il faut donc porter une attention particulière lorsqu’on
les écrit afin qu’il ne nous induisent pas en erreur.
Aussi, les tests ne doivent pas devenir un fardeau. Comme notre code, ils doivent être bien organisés et bien écrits afin
de faciliter les modifications et les ajouts. Voici donc 5 conseils à respecter lorsqu’on écrit des tests :

1. Respecter les principes du clean code. Comme le reste de notre code, nos tests doivent être propres. Pour savoir comment coder proprement
   veuillez vous référer à notre (guide sur le clean code)[lien vers le guide à venir].
2. Les tests doivent être rapides. On doit pouvoir rouler les tests souvent. Si votre code doit généralement manipuler de grands jeux de données, il vaut peut-être la peine de créer des jeux de données-jouets pour vos tests.
3. Les tests doivent être indépendants. Chaque test doit pouvoir être roulé indépendamment des autres et dans n’importe quel ordre.
4. Sortie booléenne. Un test passe ou ne passe pas. Il ne doit pas y avoir d’autres possibilités.
5. Un concept par test. Comme vous l’avez peut-être deviné en regardant les exemples, il serait possible d’écrire une seule fonction de test qui inclut tous les tests (tous les assert). Ce n’est pas une bonne pratique de faire cela. Il est recommandé de faire une fonction de test par concept. Une règle générale pourrait être de s’en tenir à un maximum de 4 assert par test et de viser un seul assert par test.

Retour sur le clean code

Comme il a été dit dans la section sur les motivations, faire des tests fait en sorte que notre code sera mieux structuré.
La raison en est très simple. Faire des tests nous incite à écrire des fonctions qui sont faciles à tester. Selon quels critères
est-ce qu’une fonction est facile à tester.

1. Elle a peu de paramètres. L’approche par l’interface sera beaucoup plus facile à faire si on n’a peu de paramètres à tester. Les deux autres approches seront aussi beaucoup plus faciles à faire s’il y a moins de combinaisons de paramètres possibles.
2. Elle fait une chose. Un de conseils que donne Robert C. Martin dans son ouvrage Clean Code, c’est d’écrire des fonctions qui ne font qu’une chose. Vous pouvez vous référer au (guide)[lien] pour savoir ce que cela signifie plus en détail. Tester nos fonctions nous incite à écrire des fonctions qui ne font qu’une chose lorsqu’on utilise la couverture basée sur la fonctionnalité. En effet, si notre fonction fait plusieurs choses, il deviendra d’autant plus difficile de répondre à la question de savoir quelle est la fonctionnalité de notre fonction. Si on n’arrive pas précisément à répondre à cette question, il sera difficile de diviser l’espace des entrées en nous base sur ce critère.
3. Elle est courte. Un autre conseil de Robert C. Martin est d’écrire des fonctions courtes (de 20 lignes maximum). La couverture basée sur les graphes nous incite fortement à faire cela. En effet, plus la fonction devient longue, plus il sera difficile de la modéliser à l’aide de graphe, plus le graphe sera gros et plus il y aura de chemins possibles à tester.